Omar Claflin

I’ve been trying to catch up on the field of interpretability these last few weeks in my free time, and have been going back over some materials that I either skimmed or simply referenced from another source. One such interesting paper/post was:

https://www.alignmentforum.org/posts/rZPiuFxESMxCDHe4B/sae-reconstruction-errors-are-empirically-pathological

Gurnee, W. “SAE reconstruction errors are (empirically) pathological.” AI Alignment Forum, March 29, 2024.

Summary: Basically, when looking at distribution tests of logit for token predictions:

KL divergence (actual, SAE reconstructed) > KL divergence (actual, random noise added)

Implying that the distribution of SAEs can be pretty bad (compared to the actual layer they are supposed to be a more interpretable replication of) even though they’ve been trained for minimal prediction loss.

(UPDATE: Larger sample test completed, results at end of post. tl;dr — this NFM + SAE improves KL divergence by about 30% over SAE alone when tested on 15M+ measurements at the end of post)

Applying this test to NFM + SAE (“Feature Integrations”)

The post link above does a much more thorough job testing multiple aspects of this logit distribution problem, but I was curious and ran a small sample set comparing: the logit KL-divergence of SAE vs SAE + NFM (vs actual and vs actual + epsilon-random noise):

“Feature Integration” reduces pathological errors by about 8.5% as measured by KL Divergence. For reference, the “Feature Integration” SAE (NFM + SAE) has about a ~23% reduction in reconstruction loss error compared to the classical SAE approach.

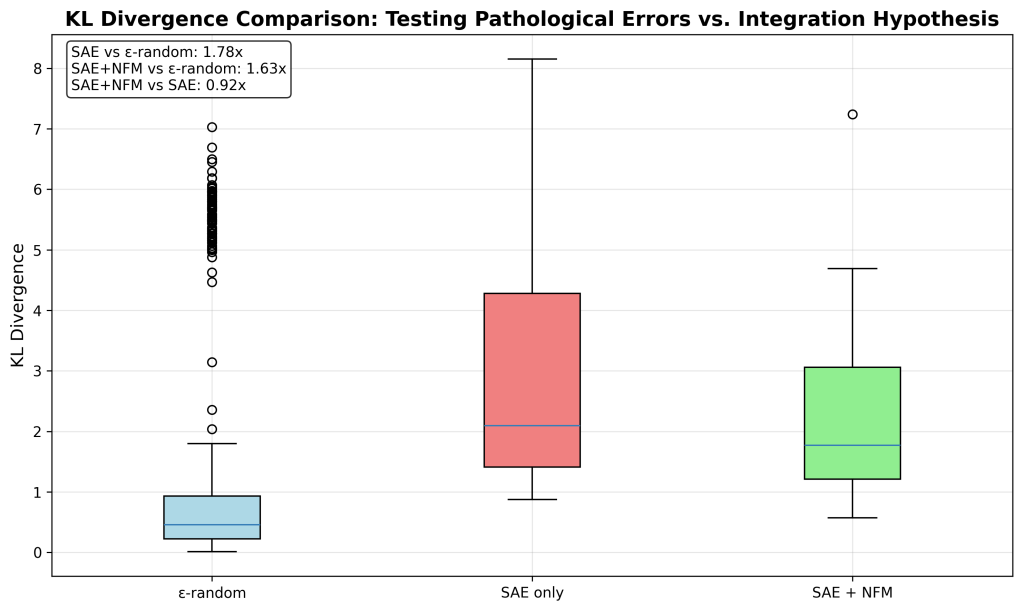
There is some promising signal here that the interactions captured by NFM may explain some of the pathology behavior of the SAE. The significance is not great (statistically) so I’m running a much larger sample currently. (Note: the epsilon-random reconstruction is included as a reproduced baseline from Gurnee’s post).

Not super impressive yet, but again, some signal.

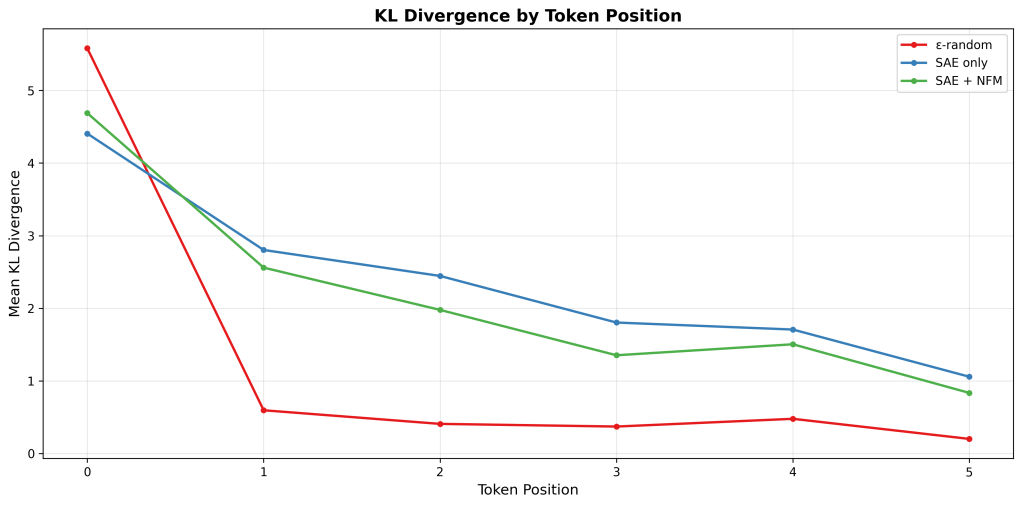
I think this roughly matches the pattern seen in Gurnee’s post (high early, drop later). Presumably, the accumulation of context (more tokens) reduces this divergence issue. Its also interesting that an accumulation of error is the opposite of what we see. It would be interesting to see with a greater statistical sample whether this first/early token prediction is similar (or worse?) with the feature integration approach. [Currently running]

There is some early signal to indicate the feature interactions not captured by SAEs (but captured by NMFs) may be some of the source.

To do list:

1. NFM methodology can be examined with linear or interactive components ‘turned off’ to see the impact first order or higher order interactions
   • Exploration of source of logit divergence by interaction source
2. Optimization and exploration of NFM training methodology to see if this KL-divergence signal can be indirectly improved
   • This early version of NFM is by no means optimized
3. Testing this on larger models, better trained SAEs, more diverse datasets, longer samples, etc
   • Currently, running this on a larger dataset (but still the small model) — will update below.
   • A well-trained SAE likely shows less NFM improvement, but the examination of this difference may be interesting

I think logit distribution makes a lot of sense as a thing to be examined (or even trained for — maybe not exactly but by rank/top N features/etc) as the pattern of probable language is meaningful to a thinking machine’s behavior & performance as final language. However, I also wouldn’t be surprised if this ordering/distribution ultimately gets captured indirectly especially when training on a similar dataset with some future improved version of an SAE (or functional equivalent).

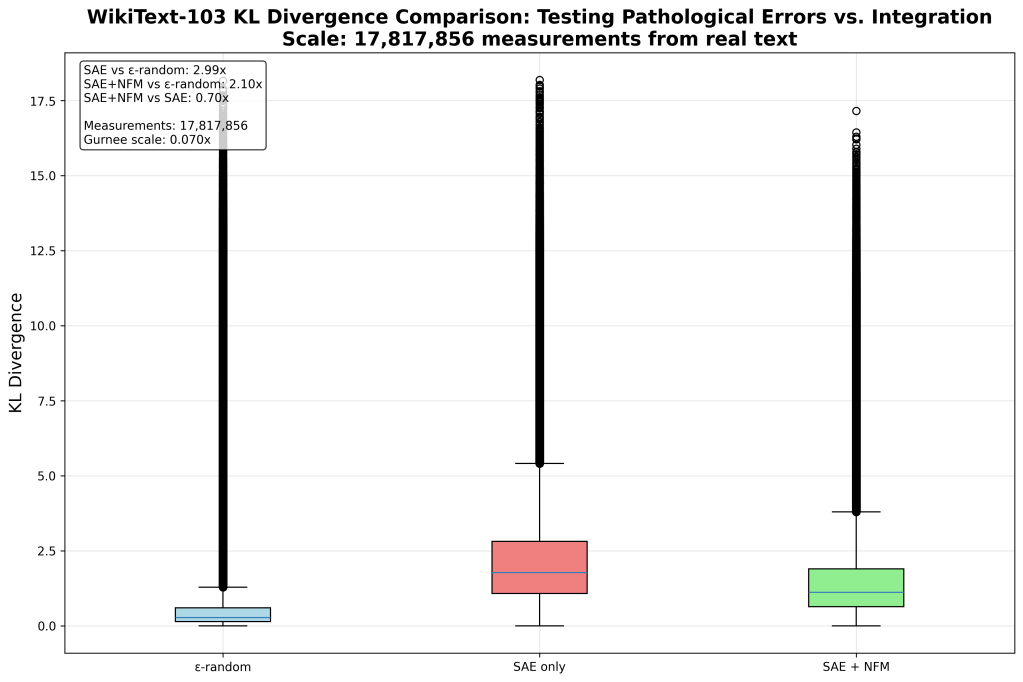
UPDATE (17M measurements; versus a couple hundred above)

Reproduction with much more samples:

Feature integration reduces pathological errors by 29.9%
This supports the hypothesis that SAE errors are due to missing feature integration
Tested on 17,817,856 real WikiText-103 measurements

Sample Size Comparison:
– This experiment: 17,817,856 measurements
– Gurnee’s scale: ~2M (x couple hundred tokens?)

Summary Statistics:
Key Ratios:
SAE vs ε-random: 2.990x
SAE+NFM vs ε-random: 2.096x
SAE+NFM vs SAE: 0.701x

Statistical Tests (t-tests):
SAE vs ε-random: t=1503.004, p=0.000000
SAE+NFM vs ε-random: t=856.750, p=0.000000
SAE+NFM vs SAE: t=-459.713, p=0.000000

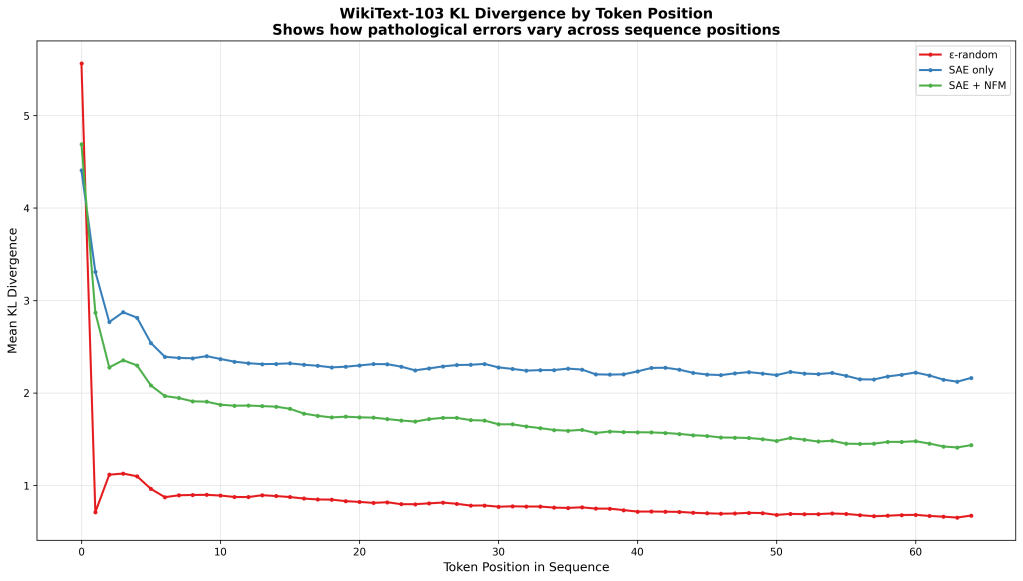
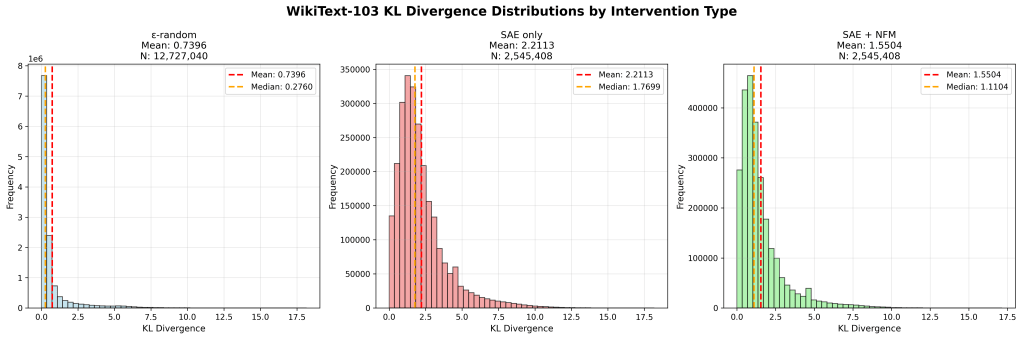
Obviously this leaves a lot of room for optimization of the NFM technique, and still finding other potential sources of ‘logit probability pathology’ but its a pretty decent signal.

I also think its interesting that the reconstruction improvement (in this particular case, more NFM+SAEs will have to be tested) is about 23% but the KL divergence test improves by about 29.9%. If:

1. KL Divergence: “How much did model ‘thinking’ change?”
2. Reconstruction Loss (L2): “How close is my final output?”

The feature relationships captured by NFM is contributing more to the next-token prediction than the L2 loss. This is exciting because small improvements in our feature relationship capture may yield larger effects on our probability space. This observation is made with a bit of caution since the effects are only shown on one model setup, but I like being optimistic.

In my somewhat biased and limited view currently, this points to the pathological errors not being about reconstruction quality alone but missing computational structure in the LLM layer that capture computational relationships. Non-linear feature interactions still has to be established as meaningfully contributing (this version only is made of about 4.5% non-linear interactions) to the KL divergence reduction.

In conclusion, for now, the reconstruction loss may be a poorer proxy for behaviorial fidelity than previously thought. Also, feature integration may have more importance for preserving model behavior that previously thought.