Omar Claflin

[Posted: https://arxiv.org/abs/2507.00269]

This post updates my previous work with a final post on my feature integration in neural networks project (previous posts) with a novel interpretability architecture that substantially improves both reconstruction fidelity and behavioral preservation.

layman’s tl;dr: Scientists attempt to read the “thinking” of AI use a technique called Autoencoders to convert raw neural signals to interpretable “thoughts.” I attempt to improve that tool which results in improved accuracy and nuance of the interpreted thoughts. Specifically, rather than just mind-reading (decoding) the words or concepts, I improve the tool so the relationships between the words or concepts can be read out as well, giving us greater access to their thoughts and explaining more of the previously undecoded neural signal.

specific tl;dr: Joint training of SAE and NFM components achieves 41.3% reconstruction improvement and 51.6% KL divergence reduction while spontaneously developing bimodal distribution of squared norm of features that validates the dual encoding hypothesis (with more subtle, distributed features contributing more to the feature interactions). The architecture also demonstrates systematic behavioral effects through controlled intervention experiments.

broad tl;dr: Typical interpretability tools of LLMs relies on autoencoders (e.g. SAEs) which use a linear decomposition technique to pull out feature identities (e.g. “Golden Gate Bridge”, a plot twist, etc) out of the neural activation space (e.g. MLP layer of an LLM). While surprisingly effective, there’s a host of problems still plaguing this approach and warping our understanding of how neural network spaces encode feature identities:

1. non-orthogonality of feature identities/currently assumed as acceptable ‘noise’ due to compressed encoding space,
2. polysemanticity [features responding to multiple concepts/words/etc]
3. a missing ‘dark matter’ of computation where [beyond recent circuit analysis approaches], it is still unknown where computation of ‘thought’ is happening,
4. “pathological” logit distributions (measured via KL divergence), revealing potentially overfit SAEs that haven’t captured the actual learned features,
5. where are the ‘inhibition circuits’ of LLM thought?,
6. is non-linear computation truly negligible?
7. other observations/inconsistencies resulting from a current point of view that might be due to missing feature integration maps

This post concludes a side project where I explore an approach (decoding feature integrations along with feature identities) in attempt to address some of these issues and provide an alternate way to think about compressed encoding of neural activations.

The Sequential Limitation

My earlier work established that Neural Factorization Machines (NFMs) could capture missing feature integration patterns, achieving 23% reconstruction improvement over standard SAEs. However, this sequential approach—train SAE first, then NFM on residuals—had fundamental limitations such as integration capture was constrained by pre-trained SAE features (retrofitting problem).

As I will show, when SAE (feature ID) and NFM (feature integrations) are jointly trained, features are allowed to naturally organize for their computational roles, and SAEs can identify lower “energy” features (lower squared norm, SAE features that are more distributed in the layer). Additionally, we see massive improvements in reconstruction loss and KL divergence over our previous sequential workflow.

Joint Training Architecture

final_reconstruction = sae_reconstruction + nfm_linear + nfm_interaction
total_loss = MSE(final_reconstruction - original_activations)

This joint optimization allows the network to develop specialized feature types naturally during training rather than forcing integration capture onto pre-existing sparse features.

Results: Multiple Validation Approaches

Reconstruction Performance

• Joint training: 41.3% improvement over TopK SAE baseline on reconstruction loss
• Sequential training: 23% improvement
• Component analysis: 94% linear, 6% nonlinear NFM parameters

Logit Distribution Fidelity (KL Divergence)

Following Gurnee’s methodology for testing logit distribution errors:

• Joint architecture: 51.6% reduction in KL divergence errors (3.2M measurements)
• Sequential architecture: 29.9% reduction (17.8M measurements)
• Statistical significance: All comparisons p<0.000001

Even our sequential architecture (previous post) showed significant improvements but the joint architecture (same number of parameters) does far better. I think of this as SAEs previously training for points rather than overall topology causing them to rotate or warp the remaining topology not included in the error metric to fit the target metric. KL divergence of logit distribution is one way we can make this previously invisible error-hiding more visible.

Emergent Feature Organization

Perhaps the most compelling finding and unexpected finding was spontaneous bimodal organization of SAE feature energy:

Standard SAE: Unimodal squared norm distribution (mean ≈ 0.4) Joint architecture: Clear bimodal separation

We see a strong spike of low squared norms very close to 0 (~0.05), and then another mode near the mean of the SAE’s distribution.

• Low magnitude features (mean ≈ 0.04): Contribute more to interaction pathways (82.8% vs 71.3%)
• High magnitude features (mean ≈ 0.37): Contribute more to direct reconstruction (28.7% vs 17.2%)

This pattern appears to emerge naturally when the architecture had flexibility to separate computational roles.

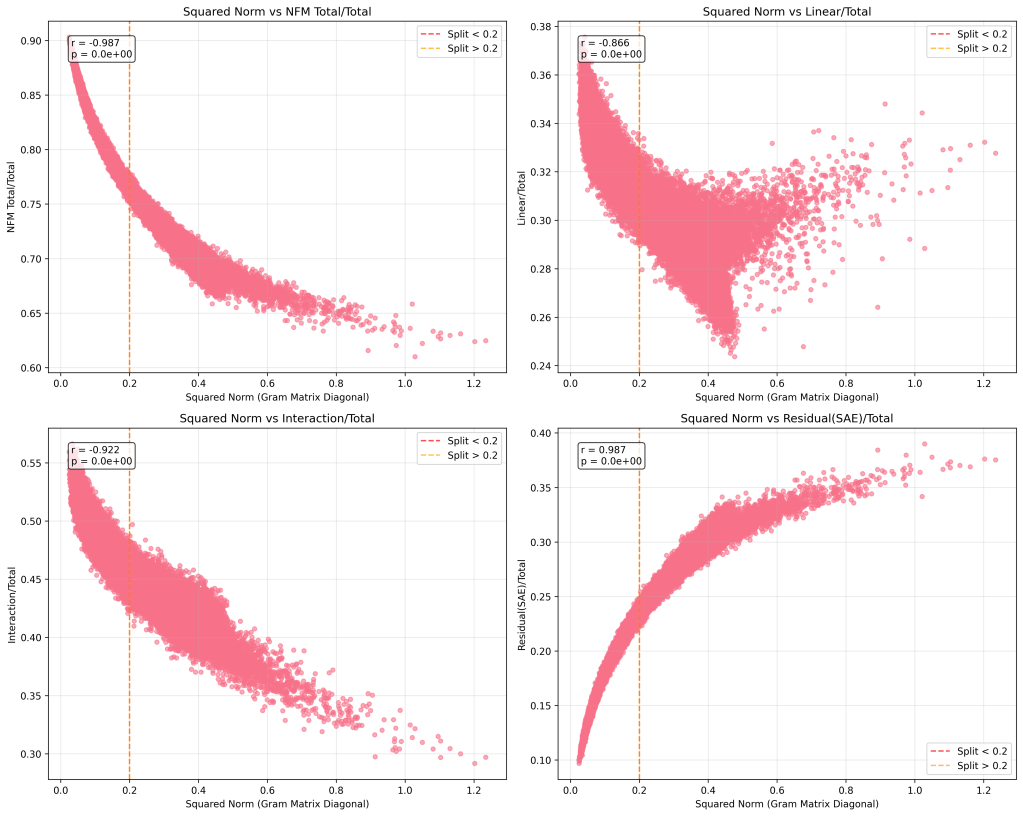
Essentially, all interaction components (linear, nonlinear, and both combined) show negative correlations (smaller magnitude SAE features contribute more to interaction features). Where higher magnitude features contribute more directly to the residual reconstruction and less to the interactions.

I could imagine this as either:

1. Capturing the previously missed, more distributed, subtle patterns (across our LLM layer) encoded in our primary SAE in our joint architecture (because they have a way to interact in our NFM components now, as it trains), picking up ‘subtler’ features previously missed
   • heavier magnitude weights ||w||² indicate features more concentrated into fewer neurons of our LLM. However, its hard to know whether these are just more concrete concepts with less interactive potential, or less defined (fusions of relationship and identity) features which avoid the interaction pathway? Of noteworthy interest, the mean of this higher squared norm population is close to our typical SAE distribution.
2. I would also expect gradient pressure of the features going through the interaction component to drive these weights down if |w| > 1, but they are |w| < 1 and still being driven down. Potentially, there’s an basic weighting mistake I’m overlooking (the activation values, TopK filtering, etc), but either way, this implies we could modify the interaction architecture to affect the pattern above (more interactions –> lower squared norms).

Behavioral Validation

We also ran systematic 2×2 factorial experiments (formal/informal × emotional/neutral) to interrogate our integration features (features within our interaction components) with selective sensitivity (covered here: https://omarclaflin.com/2025/06/23/llm-intervention-experiments-with-integrated-features-part-3/) using our sequential interaction workflow:

• ID primary features across a 2×2 stimulus set (only looking for largest main effects across primary dimensions)
• ID secondary feature which integrates these two primary features (by variance, or by ANOVA sensitivity to our 2×2 interaction)
• Generate a separate 2×2 bucket of words (I used Gemini) and target those for logit analysis
• Clamp our secondary feature, and see if our logits exhibit manipulations that are linear (main effects only) or non-linearly interactive (using an ANOVA)

With this approach, we find:

• Non-additive patterns: Clamping produced differential effects across semantic dimensions
• Some evidence of specificity: (1) A small distribution of non-zero secondary feature activations when primary features are clamped, with the outlier features being our features selected. (2) Non-significant statistical interactions when above analyses are repeated on other secondary features including highly active ones. (3) An expected non-linear interaction effect when linear interactive pathways are clamped for both primary features.

Parameter Efficiency

The nonlinear interaction component achieved disproportionate impact:

• 3% of total parameters (of total architecture) → 16.5% standalone improvement in KL divergence reduction
• Captures all higher-order feature combinations (2-way, 3-way, 4-way, etc.) in compact space
• Suggests integration patterns are sparse but functionally crucial
• However, nonlinear and linear components contribute to reconstruction improvement and KL divergence reduction sub-additively (but positive), so arguably the linear interaction component is overlapping a great deal of the same space as the nonlinear component.

Implications

Architectural novelty: This represents a move from post-hoc analysis (train SAE, analyze features and their interactions — earlier post) to integrated design (build architectures that naturally capture computational structure).

Dual-encoding hypothesis: The bimodal squared norms distribution provides direct empirical evidence that neural networks naturally separate identity and integration encoding when given architectural flexibility.

Parameter efficiency: Rather than scaling SAEs to millions of features to capture every possible interaction, targeted architectural components can efficiently capture computational relationships. Also, the computational approach we take precludes us having to explore the large computational space of (SAE number of feature)² as we train it, if we want to include interactions.

Significant non-linear encoding: While much more can be done purely with the linear interaction route, this does present a fair amount of evidence that nonlinear encoding is being captured in neural network activations. We demonstrate via interventions on selectively learned nonlinear features, as well as impressive parameter/contribution ratios (for reconstruction loss and KL divergence improvement).

• Non-linearity within the neural code has been dismissed as negligible by papers (at least that I’ve read), and perhaps been avoided due to the computational cost. However, it seems rather intuitive to me that operationally (given the explicitly non-linear actions of activation functions and attention mechanisms within transformers), and functionally (intelligent feature organization and compression of the real world would necessarily include relationships between the features that are not simple vector addition), as well as, an instrumental bias (towards computational tractable methods like SAE, which have been impressive, but are basically a linear decomposition), non-linearity most likely exists but has been overlooked.
• However, its entirely possible that much of the non-linearity captured may simply reflect an efficient way to estimate linear effects, especially as the linear and non-linear gains were sub-additive. Although, even that as an explanation still doesn’t explain away the non-linear behaviorial effects that were seen as well, so its likely present, but the significance of it is still up in the air.

Inhibition: As in human neural systems, ‘inhibitory’ circuits have been suggested but not found. Other than the advantage of separating the integration mapping from the identity mapping, which definitely architects in some specialization during learning, there is a second simpler reason that explains why this approach appears to work more effectively: negative signs. Negative signs are allowed in linear module of the feature integration mapping, whereas SAE forces all positive values (due to ReLu). In other words, concepts can combine destructively (not just constructively). While undoubtably, the SAE (and related) approaches capture some of this (‘antipodal’ axis-sharing concepts), our dictionary and computational syntax can be separately learned with the above approach. These points are irrespective of whether we consider the non-linear component. Furthermore, a secondary SAE (to learn and embed the linear feature integrations) was attempted and delivered a negligible increase in reconstruction accuracy, despite the same or higher parameter count for the SAE encoder.

Learning dynamics: One of Anthropic’s papers (“toy model”) demonstrated a type of natural geometric packing, that shifted over time, in theory, contributing to the aggregate, continuous learning curve seen during training. The underlying mechanism (theoretical, but convincing) was discrete flips/shifts in features as they, essentially, attempt to be orthogonal to each other in a compressed dimensional space that can’t allow for perfect orthogonality. Another pattern I observed in their report was a similar magnitude in the features themselves (which is responsible for the clean fairly symmetrical geometries seen; if I’m understanding it correctly). I wonder if the smaller magnitude features that emerge with a feature-interaction approach (in the smaller bimodal distribution) may therefore represent (1) pre-features not yet privileged with its own feature identity (still existing as a computation between other features), or a (2) diffuse feature vector capable of computing between features, because of its distributed magnitudes.

• This is the most speculative point (but interesting to me as a surrogate of understanding human intelligence) from this project: Combining the toy model findings and this project findings, may suggest a learning dynamic where computations between features (existing in a distributed representation) may transition into feature identities (existing in a sparse representation), within the neural representation space; or vice versa. If the approach in this project could be applied towards LLM representations during training, it may reveal fascinating learning dynamics that may broadly explain how intelligence and learning work in general, within a compressed or neural code.

What’s Next

The paper is now submitted, with code and detailed methodology available upon request. Key areas for future work:

1. Scaling validation: Testing on larger models and datasets
2. Cross-model generalization: Whether these patterns hold across architectures
3. Integration interpretability: Better methods for understanding what the interaction components compute
4. Alternative architectures: Other approaches to separating identity and integration encoding
5. Applying the Secondary SAE to the Joint NFM-SAE: I used a secondary SAE on the initial approach (sequential SAE; then NFM) to explore the feature interactions as decomposed, interpretable identities, but (for time & computational overhead reasons) never replicated this on the Joint NFM-SAE.

Broader Context

This work suggests that the “dark matter” in neural networks—computation that remains unexplained despite extensive feature analysis—may largely reflect missing integration patterns rather than inadequate feature discovery. By building architectures that naturally capture both identity and integration, we can achieve better reconstruction, better behavioral preservation, and better mechanistic understanding simultaneously.

The field has made remarkable progress in identifying what concepts neural networks represent. This work takes a step toward understanding how they compute with those concepts.

GitHub: LLM_Interpretability_Integration_Features_v2
Paper: Feature Integration Beyond Sparse Coding: Evidence for Non-Linear Computation Spaces in Neural Networks

This work was conducted independently on a home setup (RTX 3090, 128GB RAM) over a few weekends, so the code organization may be a bit sloppy.